
Since we realize that not everyone is fluent in bird-speak, perhaps it’s best if we visualize the measurements-better known as “the signal”-instead. If you are reading the paper version of this book, you’ll have to use your imagination! It goes something like this: chee-chee-woorrrr-hee-hee cheet-wheet-hoorrr-chirrr-whi-wheo-wheo-wheo-wheo-wheo-wheo. linspace ( 0, 2, 2 * f_s, endpoint = False ) x = np. So, if you take a simple periodic function, sin(10 × 2πt), you can view it as a wave: f = 10 # Frequency, in cycles per second, or Hertz f_s = 100 # Sampling rate, or number of measurements per second t = np. That, in turn, creates compressed pulses of air which, upon arrival at your eardrum, induces a vibration at the same frequency. Frequency is a familiar concept, due to its colloquial occurrence in the English language: the lowest notes your headphones can rumble out are around 20 Hz, whereas middle C on a piano lies around 261.6 Hz Hertz, or oscillations per second, in this case literally refers to the number of times per second at which the membrane inside the headphone moves to-and-fro.
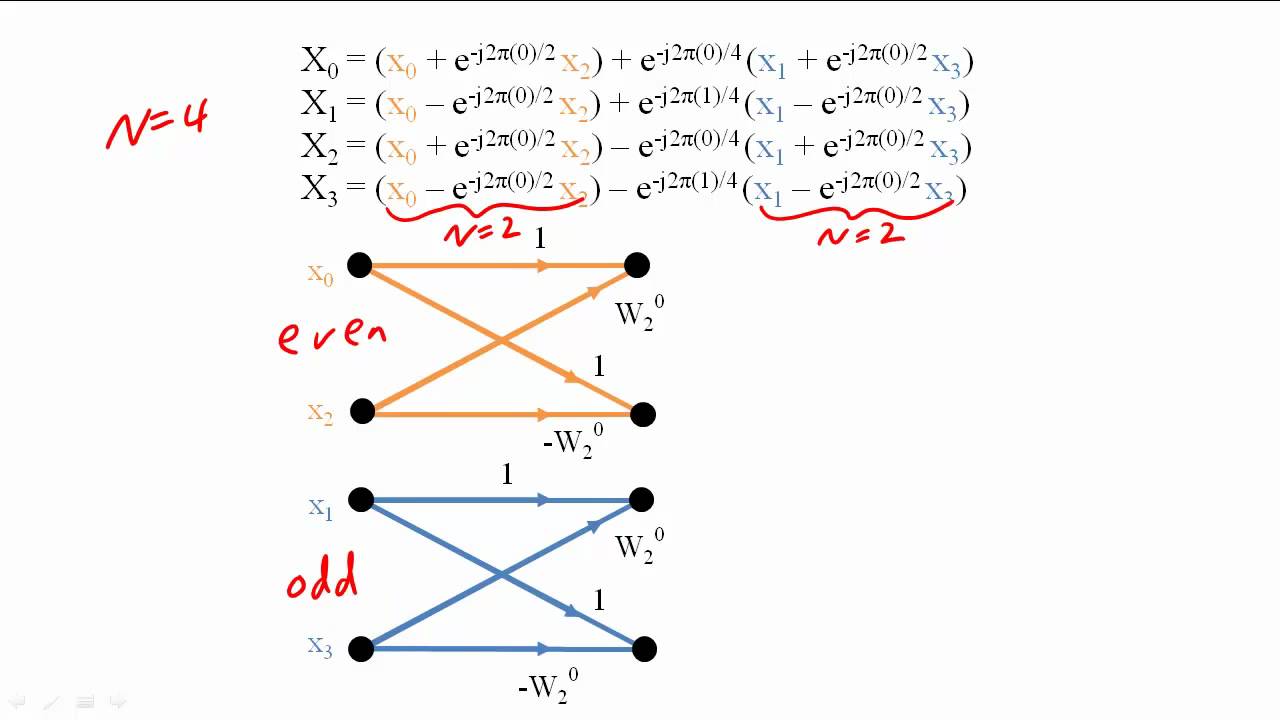
The discrete 1 Fourier transform (DFT) is a mathematical technique used to convert temporal or spatial data into frequency domain data. use ( 'style/elegant.mplstyle' ) import numpy as np We’ll start by setting up some plotting styles and importing the usual suspects: # Make plots appear inline, set custom plotting style % matplotlib inline import matplotlib.pyplot as plt plt.


 0 kommentar(er)
0 kommentar(er)
